(Number System and Operations) - part1
THREE TYPES OF OPERATIONS ON INTEGERS:
-addition & subtraction
-multiplication & division
-dealing with overflow
FLOATING-POINT REAL NUMBERS:
-representation and operations
INTEGER ADDITION(Binary Addition)
*There are four rules we should follow in binary addition as in TABLE 1
TABLE 1: The binary number operation rules
BINARY RULES
|
SUM
|
CARRY
|
0 + 0 = 0
|
0
|
0
|
0 + 1 = 1
|
1
|
0
|
1 + 0 = 1
|
1
|
0
|
1 + 1 = 0
|
0
|
1
|
EXAMPLE 1: Add these 2 numbers(101102 + 010112)
(see what is happening in each step the use the colour code)
INTEGER SUBTRACTION(Binary subtraction)
*There are four rules we should follow in binary subtraction as in TABLE 2
TABLE 2: The binary number operation rules
BINARY RULES
|
SUM
|
BORROW
|
0 - 0 = 0
|
0
|
0
|
0 - 1 = 0
|
1
|
10
|
1 - 0 = 1
|
1
|
0
|
1 - 1 = 0
|
0
|
1
|
EXAMPLE 2: Subtract 0111102 from 101012
(see what is happening in each step the use the colour code)
INTEGER MULTIPLICATION(Binary multiplication)
*There are four rules we should follow in binary subtraction as in TABLE 3
TABLE 3: The binary number operation rules
BINARY RULES
|
MULTIPLY
|
0 x 0 = 0
|
0
|
0 x 1 = 1
|
0
|
1 x 0 = 1
|
0
|
1 x 1 = 1
|
1
|
EXAMPLE 3:Multiple these two number (11112 * 10112 )
(see what is happening in each step the use the colour code)
INTEGER DIVISION(Binary division)
*Binary division follow the same procedure as binary mutiplication
EXAMPLE 4: Divide 100001 by 110
(see what is happening in each step the use the colour code)
CHAPTER 2 : Arithmetics for Computers
(Number System and Operations) - part2
NUMBER SYSTEM CONVERSION
- In this section, we will be focus only for the number system conversion of decimal, binary and hexadecimal
- Many converting method can be apply for the number system
- The most systematic method to convert the number is by using the repeated-division by base 2, 10 and 16
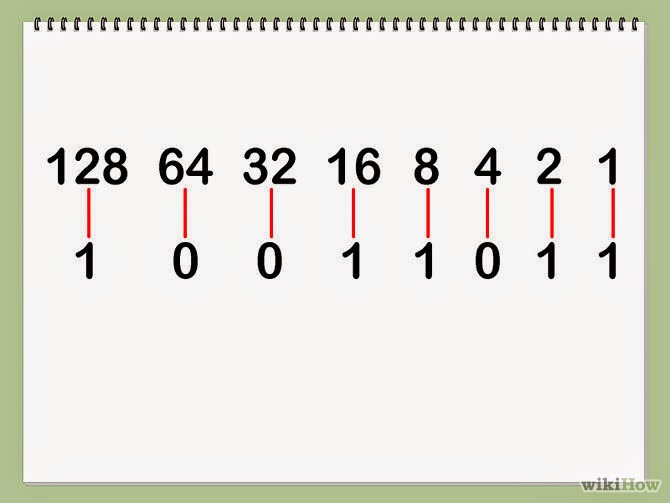
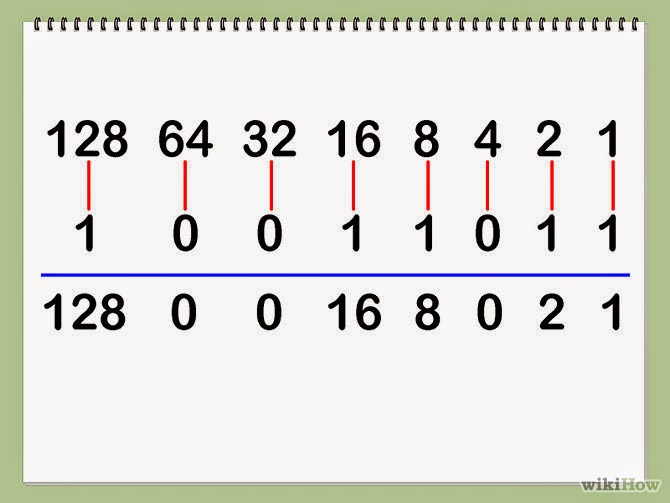
Convert binary number to decimal number
Convert decimal number to binary number
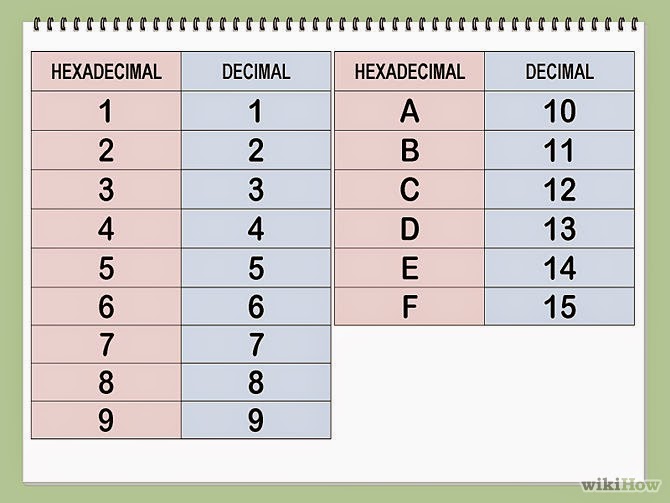
Convert decimal number to hexadecimal number
Convert binary number to hexadecimal number
Convert hexadecimal number to binary number
CHAPTER 2 : Arithmetics for Computers
(Number System and Operations) - part3
2'S COMPLEMENT NUMBER
- In microprocessor-based equipment, 2s complement method of representing numbers is commonly used
- However, microprocessor must process both positive and negative number
- The 2s complement representation used for sign and magnitude number can be determined
- Assume a microprocessor have 8 register bits
- Figure 1 show the sign bits or the most significant bit(MSB). The first bit from right is a least significant bit (LSB)
- If the MSB bit is 0, then the number is positive (+). Conversely, if the MSB is 1, yhen the magnitude is negative (-)
- The others remaining 7 bits are represent as the magnitude numbers

FIGURE 1: The MSB and LSB of an 8-bit Register Sign Bit
- For instance, a +125 is represented by the 2s complement number 01111101.
- A decimal number for -125 is represented by 2s complement number number 10000000.
- Note that the 2s complement representation for all positive value are the same as the binary equivalents for that decimal number
EXAMPLE 1: Negative Number Conversion
The negative (-) decimal number conversion is done in next step. Let's we convert
-125
STEP 1; Separate the sign and magnitude number of -1. If the sign bit is 1. it's represent as negative sign in the 2s complement conversion
STEP 2: Convert the decimal number to its 7-bits binary equivalent
DECIMAL
|
8-BIT BINARY NUMBER
|
NOTE
|
||
SIGN
|
MAGNITUDE
|
|||
+125
|
0
|
111 1101
|
Convert to 7-bits binary
|
|
000 0010
|
1st complement
|
Each 0 is changed to 1 and
each 1 to a 0
|
||
000 0011
|
2nd complement
|
Add + 1 to the 1st
complement
|
||
-125
|
1
|
000 0011
|
7-bit 2nd
complement
|
Magnitude number
|
EXAMPLE 2: Two positive integer
- 47 + 23
47 = (32 + 8 + 4 + 2 + 1) = 101111
23 = (16 + 4 + 2 + 1) = 10111
1 1 1 1 1 carry row
1 0 1 1 1 1
+ 1 0 1 1 1
1 0 0 0 1 1 1
1000110 = 70
Notice that no sign bit is added in this instance, nor is the leftmost bit to be interpreted as a negative
EXAMPLE 3: Positive Number And Smaller Negative Number
- 72 + (-100)
100 = 01100100, and the two's complement of 01100100 = 10011100
1 1 carry row
0 1 0 0 1 0 0 0
+ 1 0 0 1 1 1 0 0
1 1 1 0 0 1 0 0
There is no overflow, and the leftmost digit is a 1, indicating that the result is a negative number.
First use 2's complement to convert 11100100 to 00011011, then convert 00011011 to decimal representation and take the negative. The answer is -28
NOR EZREEN FARA BINTI KHALID - B031410024
NUR DIYANA BINTI DZOLKIFLI - B031410414
NUR SYAZWANI BINTI MAHADZIR - B031410014
NURUL HASLINDA BINTI MOHAMMAD - B031410170
NOR NURUL AIN BINTI HASSAN - B031410032